Моделирование автотранспортных потоков
проф., д.ф.-м.н. Н.Н. Смирнов, проф., д.ф.-м.н. А.Б. Киселев, В.Ф. Никитин, доцент, к.ф.-м.н. М.Н. Смирнова, инженер Д.А. Пестов

способов управления транспортными потоками.
В настоящее время организация дорожного движения является одной из основных задач городского планирования, особенно для мегаполисов, в которых количество транспортных средств на душу населения не только крайне велико, но и увеличивается год от года. Увеличение пропускной способности транспортных сетей за счет строительства и расширения автомагистралей имеет свои пределы. Первой причиной является сложность, дороговизна или невозможность расширения инфраструктуры вблизи существующей застройки (рис. 1). Второй – тот факт, что эффективность добавления новых полос движения к магистрали падает с каждой добавленной полосой из-за увеличения количества перестроений и понижения эффективности движения. Оптимизация движения в таком случае требует глубокого понимания процессов, лежащих в основе движения транспортных потоков, что может быть достигнуто за счет математического моделирования.
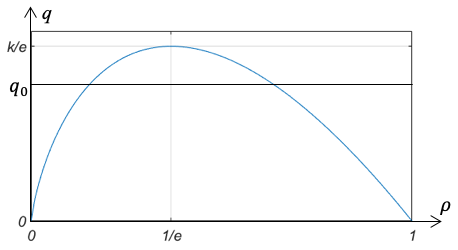
потока от плотности.
К моделированию транспортных потоков есть множество различных подходов, различающихся выбором объекта интереса, характерного масштаба или способа описания. Такими подходами могут быть исследование транспортных сетей с помощью теории графов, приближение движения отдельных машин в потоке с помощью теории клеточных автоматов или исследование транспортного потока методами механики сплошных сред.

Представление транспортного потока как сплошной среды может показаться странным, но при рассмотрении достаточно большого участка дороги поведение каждого отдельного автомобиля играет всё меньшую роль и важнее становятся осреднённые параметры, такие как плотность (отношение количества машин на выбранном участке к его длине или площади), скорость или интенсивность (произведение скорости на плотность).
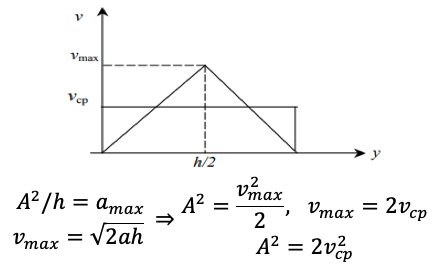
перестроении.
Использование такого подхода вместе с методами механики сплошных сред позволяет напрямую получить закономерности, лежащие в основе движения автотранспорта. Одной из таких закономерностей является так называемая транспортная диаграмма (рис 2). Здесь q – интенсивность потока, ρ – плотность (0 соответствует пустой дороге, 1 – глухой пробке), k – параметр, отвечающий за скорость реакции водителя на изменяющуюся дорожную обстановку. Из неё легко можно заметить, что одна и та же интенсивность потока qo может достигаться в двух режимах: режиме низкой плотности и режиме высокой плотности. Режим низкой плотности соответствует ситуации, когда автомобили движутся с высокой скоростью и большой дистанцией между собой. Режим высокой плотности соответствует пробке, когда автомобили движутся с низкой скоростью. Таким образом, правильная организация движения может позволить при той же пропускной способности автомагистралей обеспечить движение в режиме низкой плотности и высокой скорости.
Использование подхода механики сплошных сред позволяет описать движения транспортных потоков с помощью нескольких простых уравнений, являющихся аналогами уравнений неразрывности (1) и закона движения (2), описывающих влияние перепада плотности потока на изменение скорости потока. Дальнейшим развитием этой идеи является представление потока движущегося по многополосной магистрали как двумерной анизотропной сплошной среды [6]. В таком случае перед нами встаёт задача определения природы движения автотранспортного потока в направлении перпендикулярном направлению движения или, проще говоря, моделирования перестроений (3). На рисунках 3 и 4 показан полученный сотрудниками и студентами кафедры способ определения коэффициентов в уравнении (3), выведенный из предположительной траектории перестроения и закона изменения скоростей по время этого перестроения, а также из физических соображений того, что автомобиль при перестроении не должен терять сцепления с дорогой.
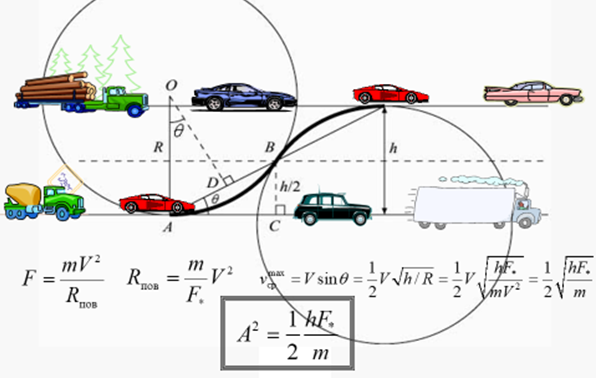
– допустимая величина боковой силы, которую можно
приложить к автомобилю без потери управляемости.
Сотрудниками кафедры также изучаются более сложные модели, такие как вязкоупругая модель транспортных потоков [2,3], модели движения по кольцевой дороге [7], вблизи перекрестка [4], в тоннелях [5,8] и методы оценки времени движения в этих условиях [9,10]. Кроме того исследуются и смежные вопросы, такие как влияние движения потока транспорта на загрязнение воздуха при движении по городу или в тоннелях [1]. Перед нами стоит множество задач, которые ещё ждут решения.
Публикации:
- Mathematical modeling of air pollution in city tunnels and evaluating mitigation strategies / M. N. Smirnova, V. F. Nikitin, D. A. Pestov, Z. Zuojin // Transportation Research Interdisciplinary Perspectives. — 2020. — Vol. 4. — P. 100086.
- Travel time prediction with viscoelastic traffic model / Z. Yongliang, M. N. Smirnova, A. I. Bogdanova et al. // Applied Mathematics and Mechanics (English Edition). — 2018. — Vol. 39, no. 12. — P. 1769–1788. DOI
- Математическая модель автотранспортных потоков с элементами вязкоупругости / M. Н. Смирнова, А. И. Богданова, Z. J. Zhu и др. // Математическое моделирование. — 2014. — Т. 26, № 7. — С. 54–64. DOI
- Математическое моделирование движения автотранспортных потоков методами механики сплошной среды / Н. Н. Смирнов, А. Б. Киселев, В. Ф. Никитин, А. В. Кокорева // Труды Московского физико-технического института. — 2010. — Т. 2, № 4. — С. 152–162.
- Freeway tunnel effect of travel time based-on a double lane traffic model / Z. Yongliang, M. N. Smirnova, J. Ma et al. // International Journal of Transportation Science and Technology. — 2021. DOI
- Multi-lane unsteady-state traffic flow models / M. N. Smirnova, A. I. Bogdanova, N. N. Smirnov et al. // Journal of Mechatronics. — 2014. — Vol. 2, no. 4. — P. 270–274. DOI
- Tunnel effects on ring road traffic flow based on an urgent-gentleclass traffic model / Y. Zhanga, M. N. Smirnova, J. Maa et al. // Theoretical and Applied Mechanics Letters. — 2021.
- Tunnel speed limit effects on traffic flow explored with a three lane model / L. Zhengming, M. N. Smirnova, Y. Zhang et al. // Mathematics and Computers in Simulation. — 2021. DOI
- Estimation of travel time through a composite ring road by a viscoelastic traffic flow model / H. Zejing, M. N. Smirnova, Y. Zhang et al. // Mathematics and Computers in Simulation. — 2021. — Vol. 181. — P. 501–521. DOI
- Travel time estimation by urgent-gentle class traffic flow model / Y. Zhang, M. N. Smirnova, A. I. Bogdanova et al. // Transportation Research Part B: Methodological. — 2018. — Vol. 113. — P. 121–142. DOI