доцент, к.ф.-м.н. Е.А. Ильюшина

Материал представляет собой результаты международного эксперимента по изучению строения атмосферных каскадов космических лучей «Памир». База данных наряду с экспериментальными содержит и искусственные данные, сгенерированные методом Монте-Карло по модели МС0 коллаборации «Памир».

Цель первого этапа работы – выбор метрики измерения расстояний и оптимального алгоритма кластеризации, при котором разбиение пятен почернения на пленке на кластеры происходит так, чтобы все пятна одного кластера соответствовали частицам одного взаимодействия, т.е., приходили с одной и той же высоты. Далее ставится задача выделения в модельных семействах отдельных групп частиц, родившихся в результате одного последнего взаимодействия. Для ее решения необходимо подобрать алгоритм кластеризации, который собирает эти частицы в один кластер с наибольшей эффективностью. Алгоритм выбирается на основе анализа модельных данных и в дальнейшем применяется к экспериментальным, поэтому необходима проверка однородности экспериментальных и модельных данных.

Произведён сравнительный анализ данных эксперимента и модели с целью получения информации, которая позволит в будущем усовершенствовать модель.

Проведены сравнения распределений физических параметров для модельных данных в зависимости от типа первичной частицы.

Рассмотрены восемь алгоритмов кластеризации, использующие различные методики выделения кластеров. Из рассмотренных методов наилучшую кластеризацию показали дивизивные методы, в частности метод кластеризации k-medoids, а именно алгоритм РАМ. Обнаружено, что алгоритм PAM не различает между собой пару метрик d1 и d3, а также d4 и d6, в то время как другие рассмотренные методы давали разные результаты для этих пар.

Для каждого типа из рассмотренных первичных частиц (ядра водорода (H), магния (Mg), кремния (Si) и железа (Fe), найдены наилучшие из шести используемых метрик. Это указывает на чувствительность применённых метрик и алгоритмов кластеризации к типу первичных частиц.

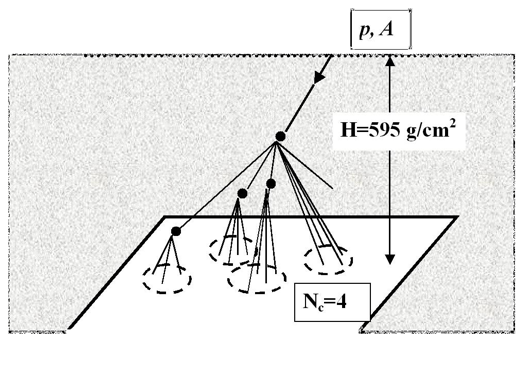
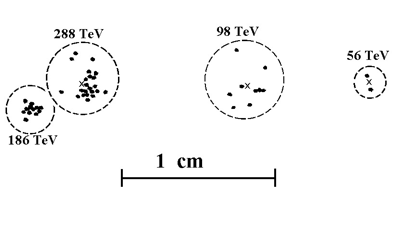
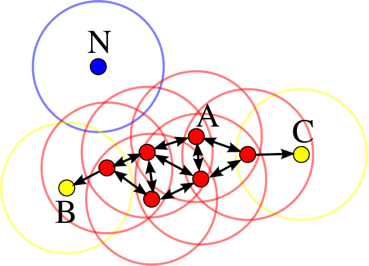
Для определения количества кластеров в среде R используется библиотека NbClust, в которой определяется экстремум каждого из девяти специальных математических индексов. Лучшим считается то количество кластеров, для которого достигается экстремум рассматриваемого показателя. Критерием выбора индекса служили среднее число ошибок метода и доля ошибок на один кластер. Наилучшие индексы - индекс достоверности стандартного отклонения и бисериальный индекс.