Космический мусор
ВЫСОКОСКОРОСТНОЕ СТОЛКНОВЕНИЕ ФРАГМЕНТОВ КОСМИЧЕСКОГО МУСОРА И СОТОВАЯ ЗАЩИТА КОСМИЧЕСКИХ АППАРАТОВ
проф., д.ф.-м.н. Н.Н. Смирнов, проф., д.ф.-м.н. А.Б. Киселев, с.н.с.,к.ф.-м.н. П.П. Захаров

Человечество ведет активную деятельность по освоению околоземного космического пространства. В 2021 году Россия произвела порядка 20 запусков, а всего в мире -более 100 запусков. Всего за 60 лет освоения космоса было запущено больше 12 тысяч космических аппаратов. На данный момент около 7 тысяч аппаратов находятся на орбите, а около 3 тысяч из них являются неработающими. Помимо крупных пассивных объектов на орбите находятся объекты меньшего размера, образовавшиеся при выводе полезной нагрузки на орбиту (ступени ракет, операционный мусор) и в результате столкновений. Все эти неуправляемые объекты и есть космический мусор, а количество его фрагментов миллионами. Фрагменты космического мусора долгие годы остаются на орбите и представляют опасность для будущих космических запусков и уже действующих аппаратов. Столкновение космического аппарата с космическим мусором с характерными скоростями порядка километров в секунду может привести к сильной поломке или полному разрушению космического аппарата.
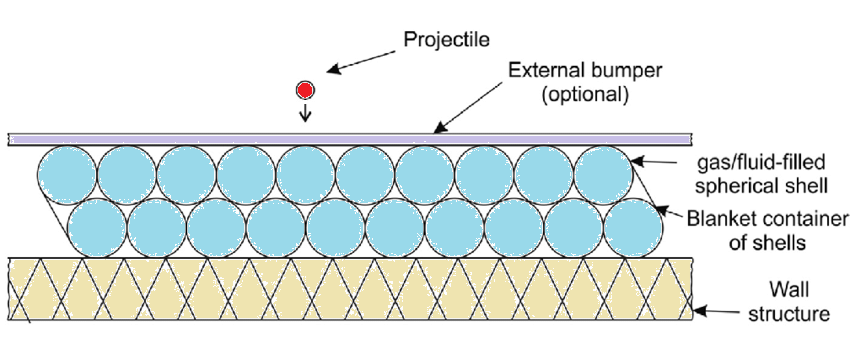
космических аппаратов.
В связи с проблемой космического мусора возникает задача механической защиты космических аппаратов от высокоскоростных мелкомасштабных фрагментов. Одной из перспективных схем защиты является сотовая конструкция, представляющая собой несколько слоев газонаполненных сфер. В результате удара кинетическая энергия фрагмента диссипирует по мере взаимодействия со слоями. Для определения эффективных параметров сотовой защиты необходимо провести компьютерное моделирование соударения фрагмента с защитой в широком диапазоне параметров задачи – скорость удара, угол, геометрические параметры сот и параметры материалов.
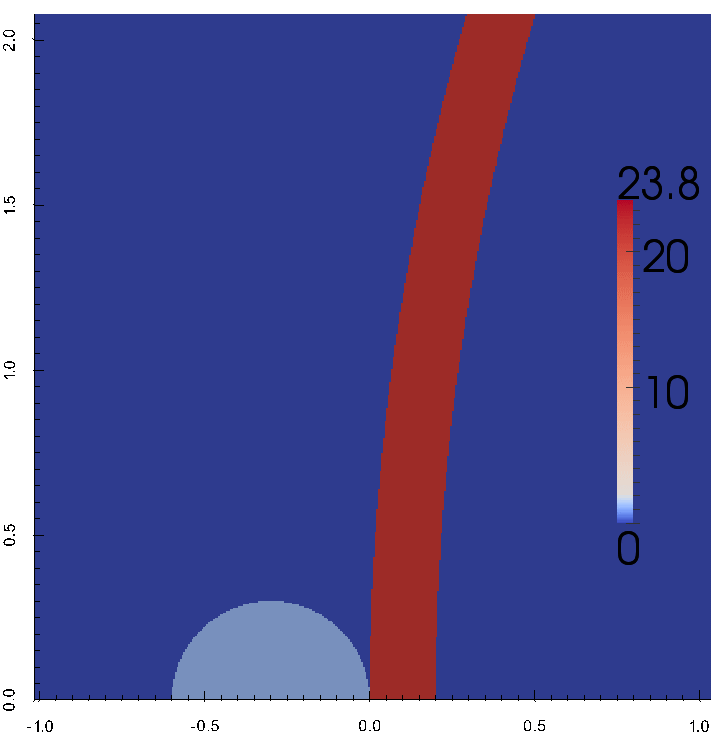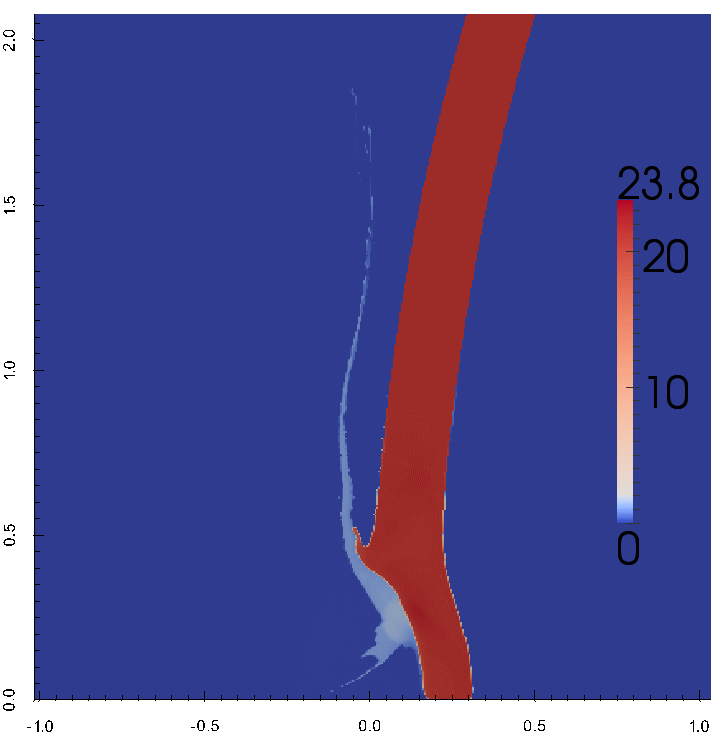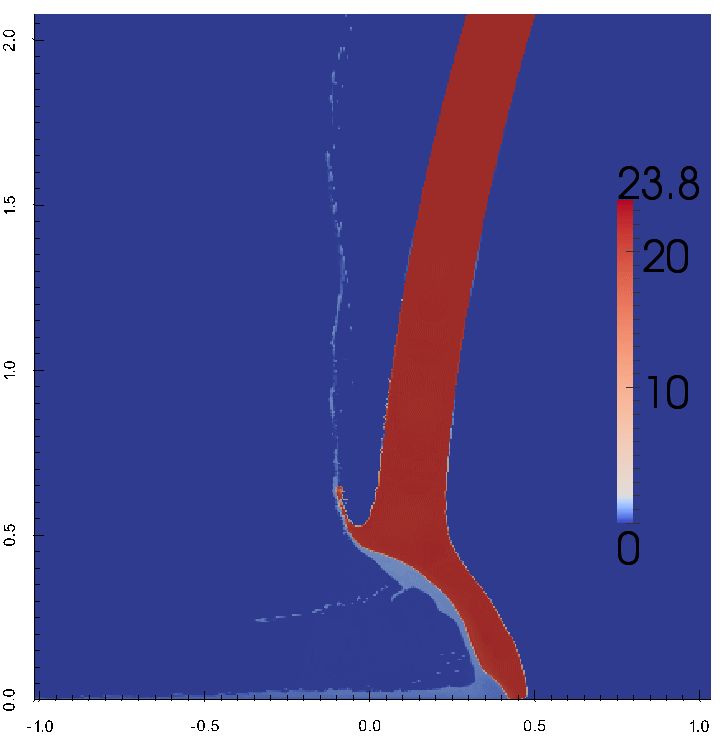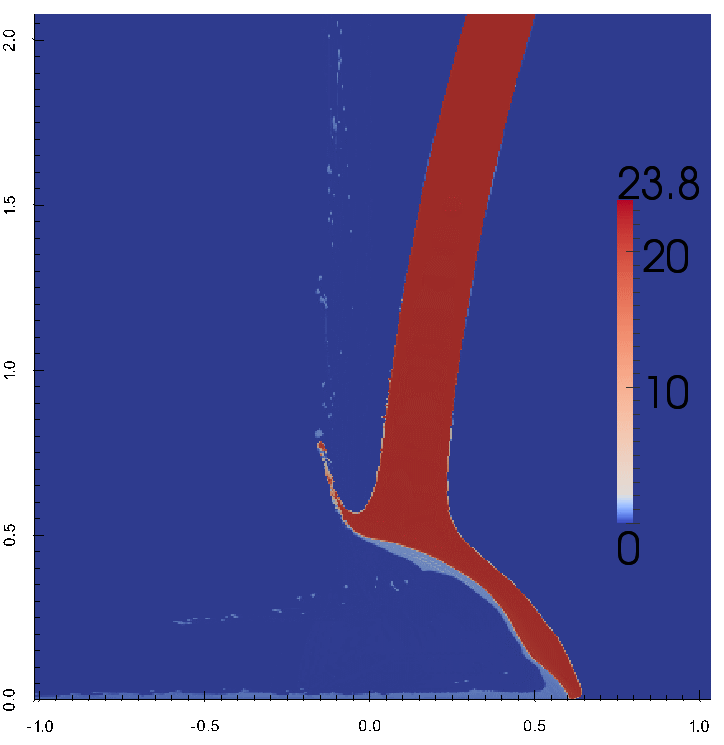
ударе низкоплотным ударником
по высокоплотной оболочке.
Такое моделирование является весьма непростым, поскольку необходимо одновременно учитывать различные физико-механические процессы в материалах конструкции - упругопластическое деформирование, плавление, фрагментация, кавитация и прочее. С другой стороны, вычислительная программа и ее численный метод должны обладать необходимой надежностью, вычислительной эффективностью и точностью. Вычислительная программа должна быть параллельной в силу разно-масштабности сотовой конструкции.
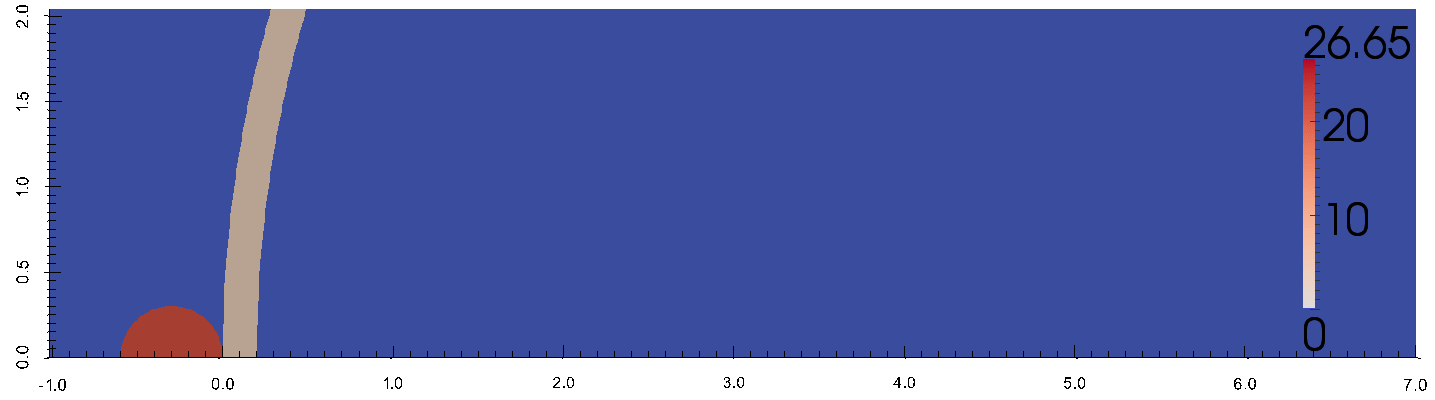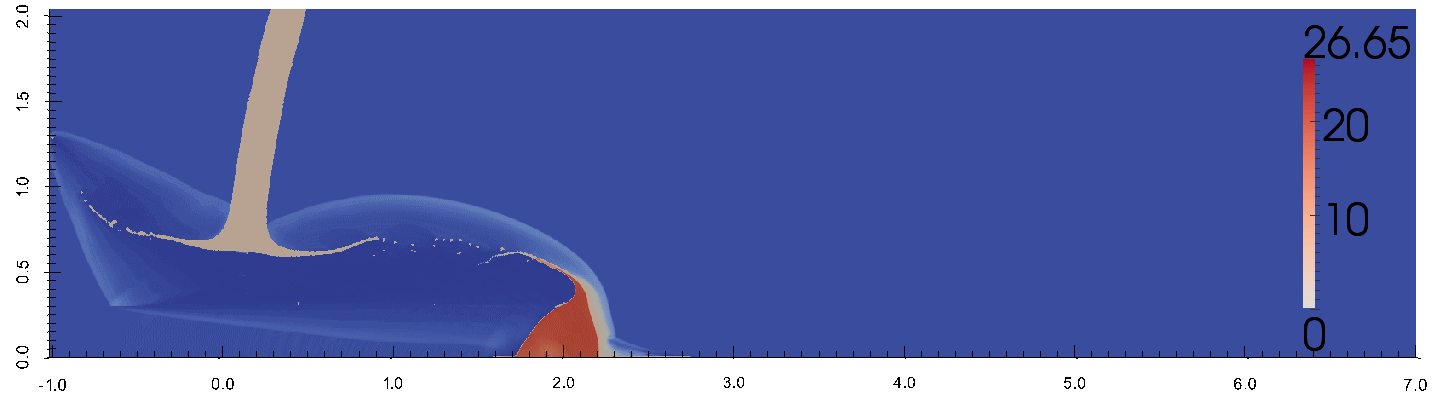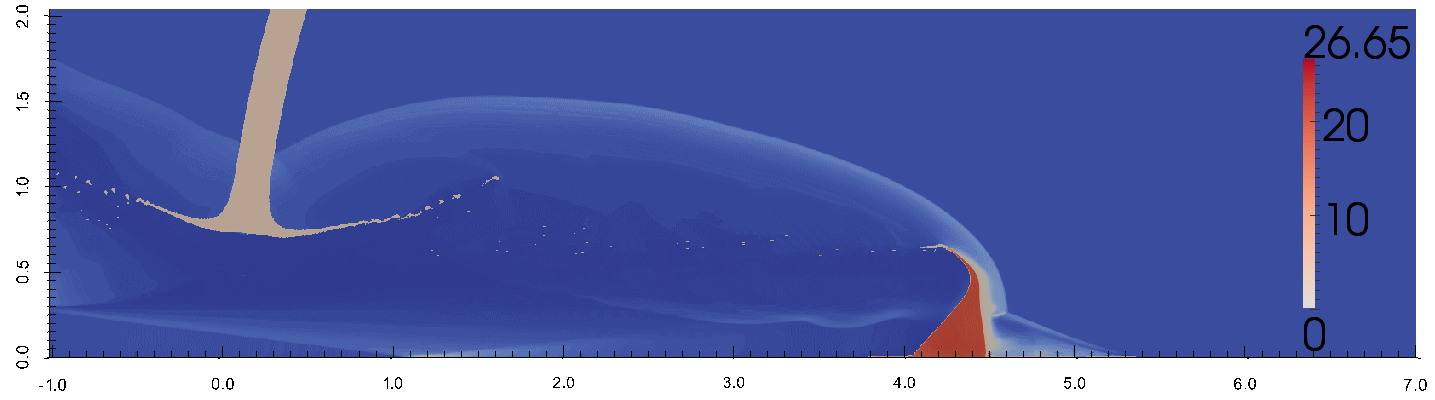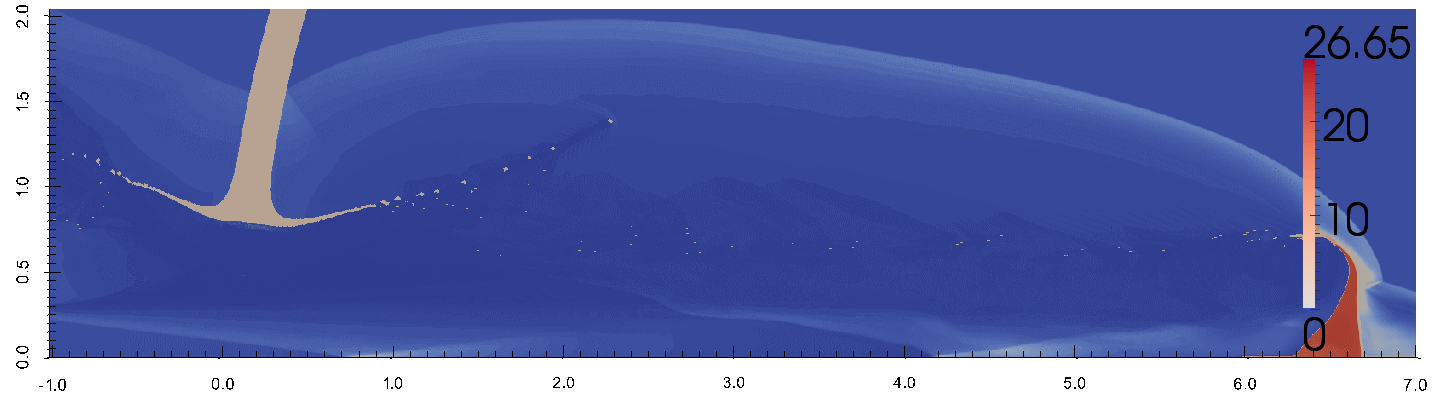
ударником.
В рамках выполнения работ по данной теме сотрудниками кафедры проводится численное моделирование высокоскоростного столкновения фрагмента космического мусора в двумерной осесимметричной постановке. Численный метод, лежащий в основе, вычислительной программы является Эйлеровым конечно-объёмным методом сквозного счета. Аппроксимация численных потоков осуществляется методом С.К. Годунова. Для преодоления вычислительной проблемы, обоснованной разномасштабностью задачи, используются динамические локально-адаптивные сетки. В параллельном расчете с распределенной памятью используется алгоритм балансировки вычислительной нагрузки, который меняет геометрические размеры декомпозиции расчетной области.
адаптацией.
Публикации:
- N. N. Smirnov, A.B. Kiselev, V.F. Nikitin, Investigation of High-speed Collisions of Space Debris Particles with Gas-filled Shells, 2003 Moscow University Mechanics Bulletin, Allerton Press. (Vestnik Moskovskogo Universiteta. Ser. 1 Matematika Mekhanika) (1), pp. 54–66. DOI
- N. N. Smirnov, A. B. Kiselev, P. P. Zakharov, Numerical simulation of the high-speed collision of the ball and the spherical fluid-filled shell, Acta Astronautica. 163 (2019) 62-72.DOI
- N. N. Smirnov, A. B. Kiselev, P. P. Zakharov Numerical simulation of the hypervelocity impact of the ball and the spherical containment in three-material statement, Acta Astronautica. 171 (2020) 215-224.DOI
- N. N. Smirnov, A.B. Kiselev, P.P. Zakharov, R.V. Muratov, D.M. Bukharinskaya. The usage of adaptive mesh refinement in simulation of high-velocity collision between impactor and thin-walled containment. Acta Astronautica. (2021) DOI
- P. D. Anz-Meador, V. A. Chobotov, W. Flury, A. B. Kiselev, A. I. Nazarenko, V. F. Nikitin, A. E. Potter, N. N. Smirnov, T. Yasaka, Space Debris. Hazard Evaluation and Mitigation, United States, Taylor and Francis, 2002.
- N. N. Smirnov, A. B. Kiselev, K. A. Kondratyev, S. N. Zolkin, “Impact of debris particles on space structures modelling,” Acta Astronautica, vol. 67, no. 3-4, pp. 333–343, 2010.DOI
ПРИМЕНЕНИЕ ТРОСОВЫХ СИСТЕМ ДЛЯ ОЧИСТКИ ОРБИТЫ ОТ КОСМИЧЕСКОГО МУСОРА
проф., д.ф.-м.н. Н.Н. Смирнов, в.н.с., д.ф.-м.н. А.А. Малашин, инженер, к.ф.-м.н. П.А. Дьяков
Применение тросовых систем в космосе является одним из наиболее динамично развивающихся направлений по освоению космического пространства. Это связано, в первую очередь, с широким кругом задач, которые можно решать при помощи тросовых систем без существенных топливных и энергетических затрат. С помощью таких систем возможно выполнять межорбитальное маневрирование, перемещение полезной нагрузки между орбитами или космическими аппаратами, возращение грузов с орбиты на Землю (космическая почта), борьба с космическим мусором, увод отработавших аппаратов с орбиты.
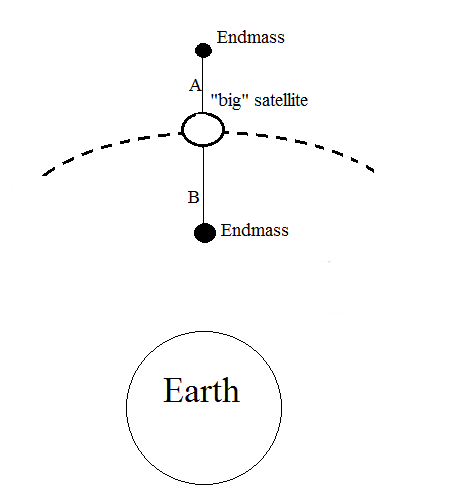
орбите.
Один из вариантов "уборки" орбиты от космического мусора предполагается следующим образом. На орбите, которую необходимо очистить от мусора, размещается головной спутник – ловушка, на который доставляются «пойманные» на орбите фрагменты мусора. Вниз и вверх от головного спутника выпущены гибкие растяжимые тросы с закрепленными массами на концах (Рис. 6). Подобная конфигурация обеспечивает устойчивое положение системы на орбите. При накоплении достаточного количества частиц мусора, он помещается в капсулу, которая начинает перемещаться от головного спутника к оконечным массам. При достижении концов троса, капсулы с мусором могут накапливаться, увеличивая оконечную массу или же выпускаться на орбиту захоронения, или сбрасываться в атмосферу Земли, где и сгорят (в случае низких орбит).
Сложное движение оконечных масс, нагрузки по тросу и самого троса неизбежно приведет к возникновению нежелательных продольно - поперечных колебаний троса, которые могут привести к нарушениям конфигурации системы - обрывам троса, сильным отклонениям нагрузки и оконечных масс. В рамках исследований сотрудниками кафедры был получен ряд результатов по обеспечению устойчивости функционирования подобных систем, оценке влияния волновых процессов в тросе на общую динамику системы на разных этапах, разработке методологии по моделированию общей динамики системы с учетом волновых процессов в тросе. Полученные результаты могут быть использованы при расчете реальных орбитальных миссий с применением тросовых систем.
Публикации:
- Diakov P. A., Malashin A. A., Smirnov N. N. Problem of load transportation along a space tethered system // Acta Astronautica. — 2018. — Vol. 150. — P. 44–48. DOI
- Diakov P. A., Malashin A. A., Smirnov N. N. Dynamic processes in the tether of a space tethered system // Acta Astronautica. — 2019. — Vol. 163, no. A. — P. 100–106.DOI
- Diakov P. A., Malashin A. A., Smirnov N. N. Estimation of parameters of the space tethered system for stable load transportation along the tether // Acta Astronautica. — 2021. —Vol. 181. — P. 602-605.DOI