Плоские задачи движения тел вблизи границ раздела сжимаемых сред
доцент, к.ф.-м.н. М.Н. Смирнова, проф., д.ф.-м.н. А.В. Звягин

крыльях «Комета».
Движение тел вблизи поверхности раздела различных сред является основой работы многих технических устройств, например, движение тел под свободной поверхностью жидкости: подводных крыльев, а также пуль, торпед, реактивных снарядов. Близость свободной поверхности существенно влияет на силу сопротивления и подъемную силу крыла.

К данному классу задач относятся также задачи движения частиц космического мусора в контейнерах с жидкостью. Решение задач взаимодействия высокоскоростных фрагментов космического мусора с частично заполненными жидкостью контейнерами, окружающими космические аппараты, необходимо для адекватного прогнозирования функционирования орбитальных конструкций.
И задачи движение крыльев в сжимаемых средах вблизи жестких границ. Подъемная сила крыла при приближении к жесткой поверхности (земле) существенно возрастает. Этот эффект успешно используется при создании экранопланов – летающих объектов, движущихся вблизи поверхности Земли или над водным пространством.

Для решения перечисленных задач необходимо проведение предсказательного моделирования процессов движения тел в сжимаемых средах вблизи подвижных или жестких поверхностей раздела на высокопроизводительных ЭВМ, написание программ для которых требует значительного времени и усилий, а сами коды нуждаются в верификации. Поэтому получение точных аналитических решений указанных задач для случаев упрощенной геометрии – необходимая составляющая создания верификационного базиса разрабатываемых отечественных программных продуктов типа ЛОГОС и Лэгак ДК Росатома.

Были исследованы задачи плоского дозвукового движения тонких тел в сжимаемой жидкости вблизи свободной поверхности и твердой границы.
При движении тела в жидкости под свободной поверхностью были рассмотрены случаи образования каверн бесконечного и конечного размеров, а также крылья двух типов: вогнутое и выпуклое. Построено аналитическое решение, позволяющее найти величину силы сопротивления и подъёмной силы крыла в предельных случаях малой и большой глубины.
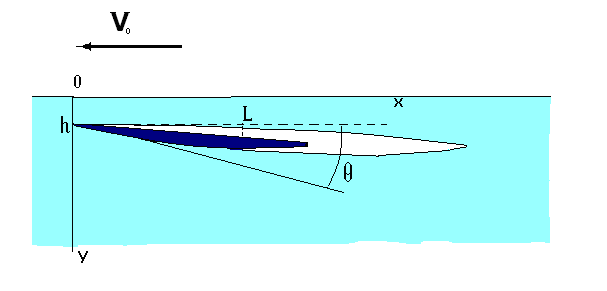
на глубине h с постоянной скоростью Vo
под заданным углом атаки.
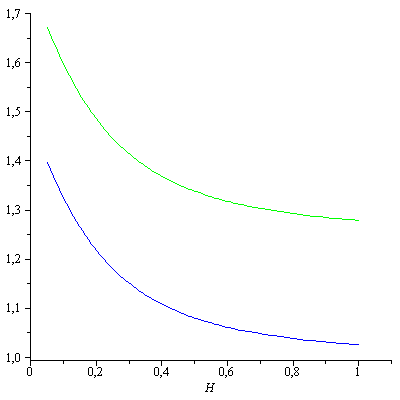
силы от безразмерной высоты для пластины
(кривая синего цвета) и для выпуклого
контура (кривая зелёного цвета).
При движении вблизи твердой поверхности были рассмотрены случаи крыла в виде пластины и в виде выпуклого контура. Задачу движения крыла около твердой поверхности (экрана) в линейной постановке удалось решить почти аналитически: полученная подъёмная сила отличается от аналогичной величины для неограниченного пространства дополнительным слагаемым, которое убывает с увеличением расстояния от крыла до поверхности. Была получены зависимость приведённой подъёмной силы FПδ/ρoVo2πγL от безразмерной высоты H=h·δ/L, δ=√1-M2для пластины (кривая синего цвета) и для выпуклого контура (кривая зелёного цвета).
Проведенный расчет показывает, что экран заметно влияет на подъемную силу только на высоте полёта, меньшей длины хорды крыла, а подъёмная сила быстро убывает с увеличением высоты до величины, равной её значению в безграничной среде, полученному Н.Е. Жуковским FП=ρoVo2πγL/δ. Подъёмная сила выпуклого крыла больше подъёмной силы пластины для соответствующих расстояний от экрана.
В ходе численного решения задачи движения пластины вблизи твердой поверхности методом граничных элементов было проведено сравнение полученной зависимости подъемной силы от высоты с аналитическим решением. Были построены линии тока и распределение скорости вдоль них при обтекании пластины с разными углами атаки и на разном расстоянии от экрана.
Публикации:

- Звягин А.В., Смирнова М.Н. Движение тонкого тела вблизи свободной поверхности сжимаемой жидкости // Вестник Московского университета. Серия 1. Математика, механика, 2009. – №2, с. 35-44. (Engl. transl.: Zvyaguin A.V., Smirnova M.N. Motion of a slender body near the free surface of compressible fluid // Moscow University mechanics Bulletin, 2009. – vol. 64. – №2. – pp. 5-15).
- Smirnova M.N., Zvyaguin A.V. Fluid flow interaction with an obstacle near free surface // Acta Astronautica, 2009. – v. 64. – pp. 288–294. DOI
- Smirnova M.N., Zvyaguin A.V. Different flow scenario for thin body subsonic motion in compressible fluid under free surface // Acta Astronautica, 2010. – vol. 66. – pp. 434 – 438. DOI
- Smirnova M.N., Zvyaguin A.V., Shugan I.V., Ray-Yeng Yang, Hwung-Hweng Hwung. Thin body motion under free surface with formation of final length cavity // Acta Astronautica, 2011. – v. 68. – iss. 1-2. – pp. 46-51. DOI
- Smirnova M.N., Zvyaguin A.V. Theoretical solution for the lift force of “ecranoplan” moving near rigid surface // Acta Astronautica, 2011. – v. 68. – iss. 11-12. – pp. 1676-1680. DOI
- Smirnova M.N., Zvyaguin A.V. High velocity motion of a wing in compressible fluid near a surface // WSEAS Transactions on Fluid Mechanics, 2011. – v. 6. – iss. 2. – pp. 92-101
- Smirnova M.N., Kondrat’ev K.A. Space debris fragments impact on multi-phase fluid filled containments // Acta Astronautica, 2012. – v. 79. – pp. 12-19.DOI
- Smirnova M.N. Mars transportation vehicle concept // Acta Astronautica, 2014. – v. 103. – pp. 250-256.DOI
- Smirnova Maria N., Riccardi Giorgio. Thin body motion in compressible fluid in the presence of free and rigid boundaries // European Journal of Mechanics, B/Fluids, 2017. – v. 62. – pp. 1-11. DOI