проф., д.ф.-м.н. Н.Н. Смирнов, В.Ф. Никитин, н.с. Е.В. Михальченко, к.ф.-м.н. Я.М. Карандашев, к.ф.-м.н М.Ю. Мальсагов

Во многих случаях задача расчета газодинамических процессов в двигателях, силовых установках включает моделирование физических и химических взаимодействий. В полномасштабном трехмерном моделировании современных и перспективных ракетных двигателей часто используются топлива, которые описываются подробными химическими механизмами, включающими сотни, а иногда и тысячи элементарных реакций между десятками и сотнями компонент. Объединение вычислительной газодинамики и моделирование горения является сложной вычислительной задачей из-за необходимости объединения нелинейных уравнений химической кинетики с уравнениями газодинамики и явлениями переноса. Узким местом всего подхода является расчет химической кинетики, который требует интеграции стадии решения жесткой системы обыкновенных дифференциальных уравнений в численный процесс с мелким шагом по времени. Прямая интеграция подробных химических механизмов с большим числом компонент и реакций в трехмерные газодинамические задачи в настоящее время ограничена доступными вычислительными ресурсами.

Чтобы сократить время вычислений, многие программные коды используют сокращенные кинетические механизмы. Существуют различные методы получения редуцированных механизмов из подробных данных: Вычислительное одиночное варьирование (CSP, Computational Singular Perturbation); Внутренние низко-размерные многообразия (ILDM, Intrinsic Low Dimensional Manifolds); Уровень значимости (LOI, Level of Importance); Программа компьютерного сокращения механизма (CARM, Computer Assisted Reduction Mechanism Code) ; Ограниченное равновесие, определяемое интенсивностью реакций (RCCE, Rate Controlled Constrained Equilibrium); Направленный граф отношений (DRG, Directed Relation Graph), и т.д. При использовании сокращенных механизмов необходимо выбрать правильный механизм для задачи рассматриваемого, чтобы соблюсти ограничения механизмов в выбранных диапазонах параметров. Но даже при значительном сокращении кинетический шаг использует значительную часть общего времени вычислений.

Другими способами сокращения времени вычислений являются методы, в которых термохимическое состояние пространства вычисляется во время моделирования и сохраняется в таблицах для дальнейшего повторного использования.

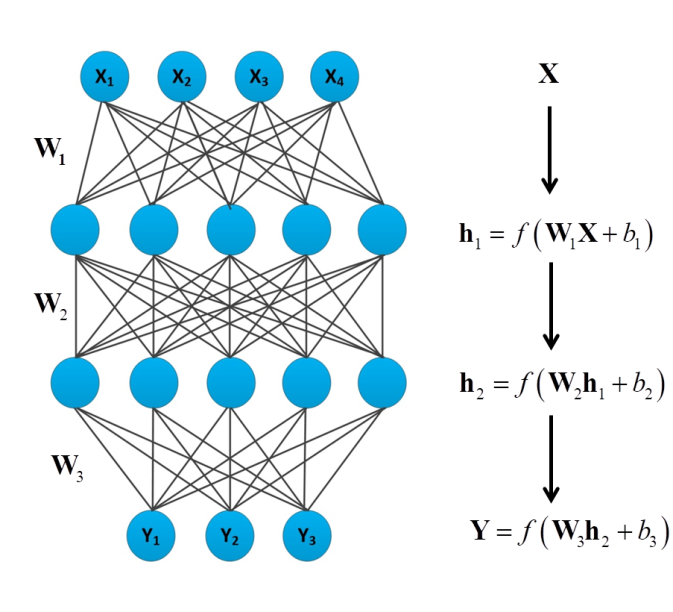
В настоящее время подход с использованием нейронных сетей (Рис.1) является многообещающим для ускорения такого рода вычислений. Методы машинного обучения получили широкое распространение благодаря многочисленным достижениям в алгоритмах и доступности вычислительных мощностей.

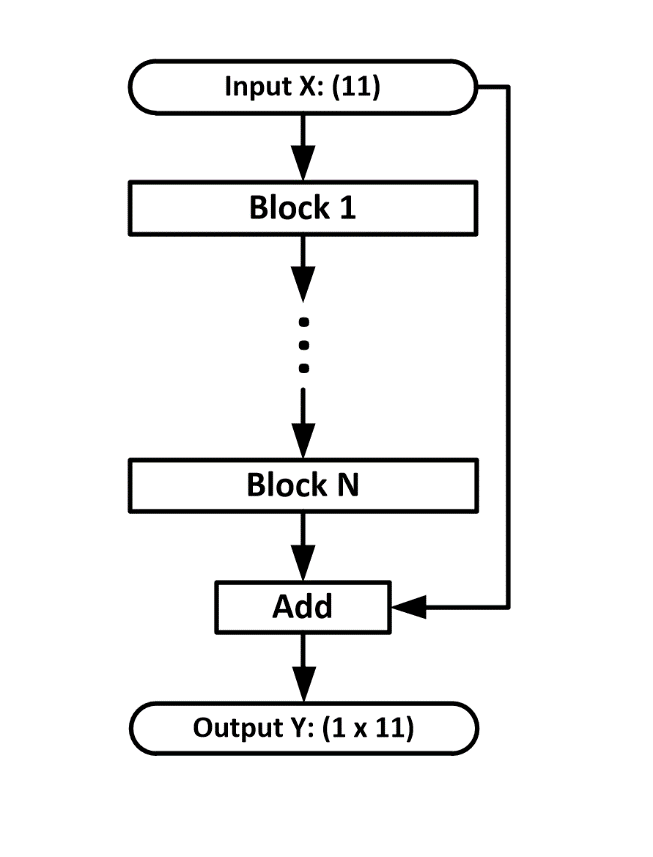
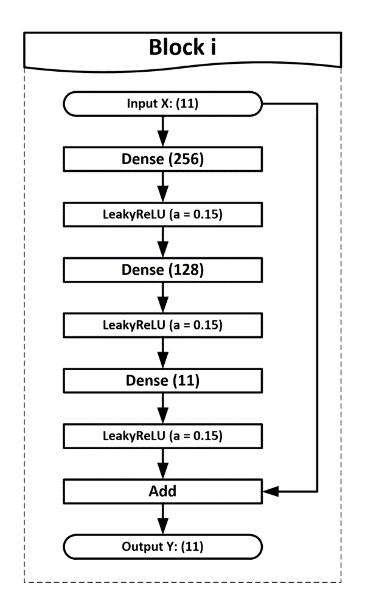
Архитектура нейронной сети представлена на рисунке 2. Входом сети является вектор размерности 11, то есть состояние химической системы (температура и молярные плотности веществ). Вход передается через несколько одинаковых блоков, состоящих из нескольких слоев. Затем результат покомпонентно складывается с входом и передается на выход сети.

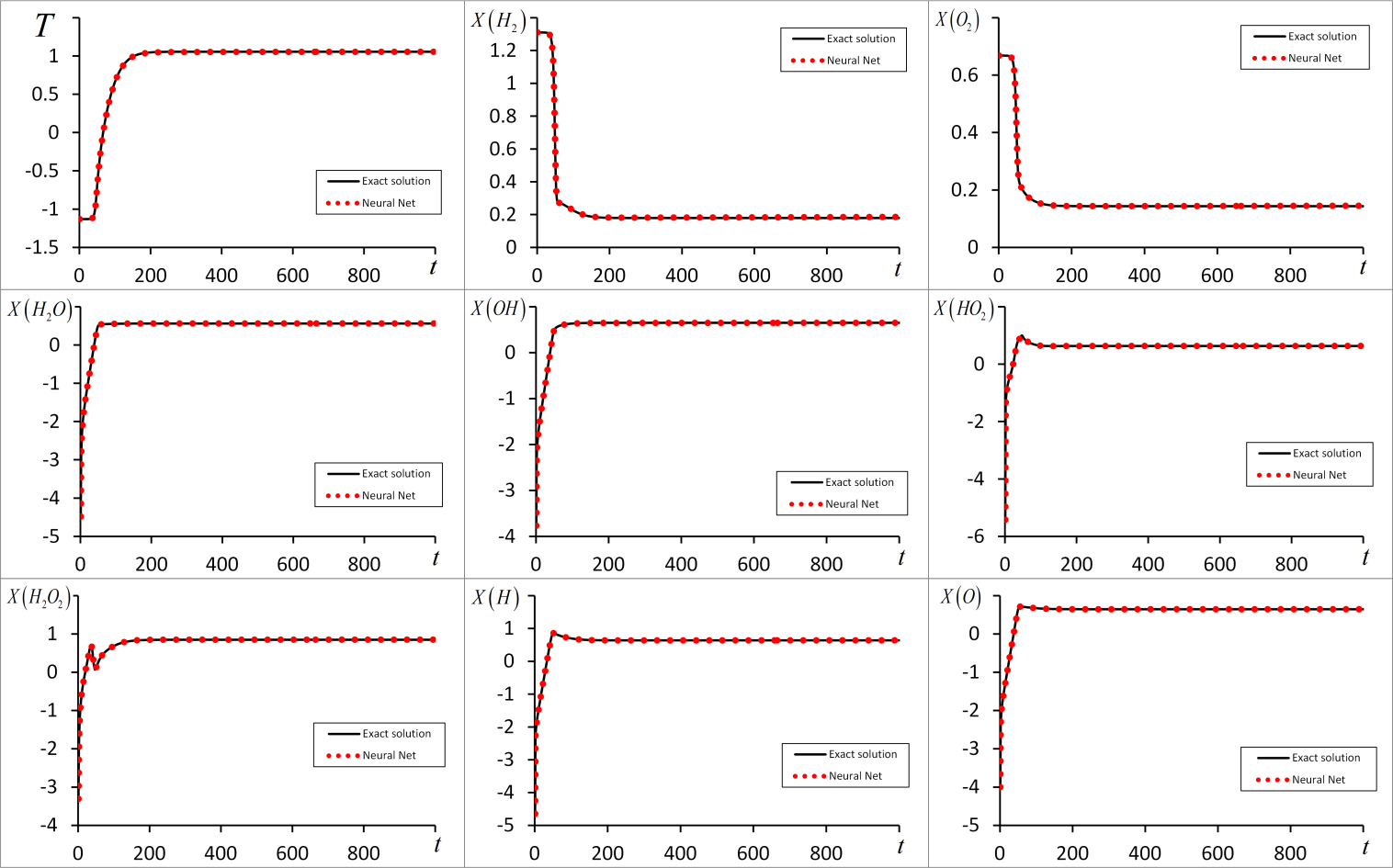
На рисунке 3 представлен результат работы сети с девятью блоками. Маркерами изображены результаты нейронной сети, а сплошная линия – эталонные значения, которые сеть должна была получить. На рисунке видно, что обученная сеть неплохо может предсказывать развитие процесса горения на 1000 шагов, без заметного нарастания ошибки при циклическом процессе работы. В данном примере ошибки прогноза оказались следующими: MAE=0.0014, MSE=4.415·10^-6.

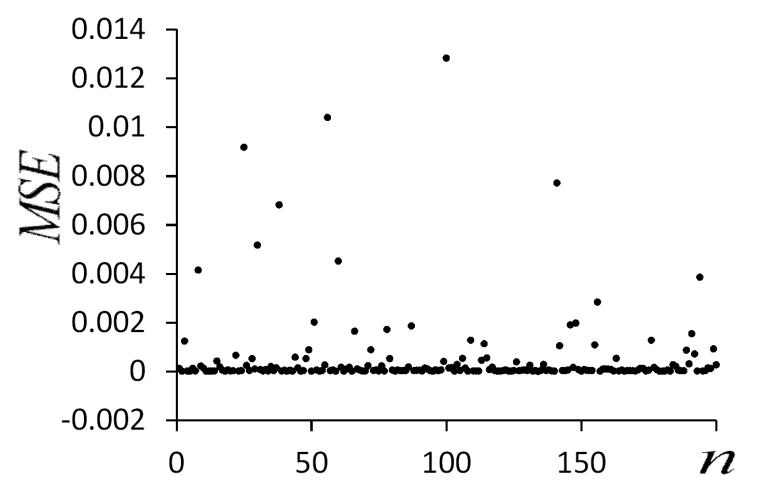
На рисунке 4 показано, как менялась среднеквадратичная ошибка при 200 случайных экспериментах. Как видно из рисунка, большая часть экспериментов дает хороший результат, ошибка близка к нулю. Перечисляя и настраивая различные архитектуры многослойных нейронных сетей, можно получить относительно простую модель, способную решить проблему. Полученная нейронная сеть может предсказывать развитие химической системы, состоящей из большого числа компонент, на много шагов вперед, работая в рекурсивном режиме. Более того, вычислительная сложность модели практически не зависит от количества веществ, участвующих в реакции. Моделирование нейронной сети может частично или полностью заменить дорогостоящие вычислительные методы численного моделирования при сохранении количественно точных результатов.

Публикации:

1. V. F. Nikitin, I. M. Karandashev, M. Yu Malsagov, E. V. Mikhalchenko. Approach to combustion calculation using neural network. Acta Astronautica, 2021.DOI
2. V. B. Betelin, B. V. Kryzhanovsky, N. N. Smirnov, V. F. Nikitin, I. M. Karandashev, M. Yu Malsagov, E. V. Mikhalchenko. Neural network approach to solve gas dynamics problems with chemical transformations. Acta Astronautica, 180:58–65, 2021. DOI
3. Б. В. Крыжановский, Н. Н. Смирнов, В. Ф. Никитин, Я. М. Карандашев, М. Ю. Мальсагов, Е. В. Михальченко. Использование нейронных сетей для моделирования задач горения. Успехи кибернетики, 4(2):15–29, 2021.
4. Я. М. Карандашев, Е. В. Михальченко, М. Ю. Мальсагов, В. Ф. Никитин. Моделирование динамики горения водорода при помощи полносвязной нейронной сети unet. Суперкомпьютерные дни в России : Труды международной конференции. 27–28 сентября 2021 г., Москва / Под. ред. Вл. В. Воеводина, стр. 161–162. Москва: МАКС Пресс, 2021.