Разработка математических моделей и методов увеличения нефтеотдачи
НЕФТЕГАЗОВЫЕ ТЕХНОЛОГИИ
доцент, к.ф.-м.н. М.Н. Кравченко
Развитие нефтегазового комплекса страны – это задача, которую активно решают не только производственники, но в первую очередь ученые. Роль механико-математического факультета МГУ им. М.В. Ломоносова трудно переоценить, если говорить о создании теоретической базы разработки месторождений нефти и газа. Ученые МГУ принимали самое деятельное участие в создании принципов теории разработки. Один из учеников самого Н.Е. Жуковского, ставший профессором МГУ им. М.В. Ломоносова, академиком АН СССР, Л.С. Лейбензон со своими учениками заложили основы отечественной нефтегазовой науки. Возглавляя кафедру гидромеханики и затем основав кафедру упругости на механико-математическом факультете МГУ, с 1922 Л.С. Лейбензон в качестве профессора работал одновременно и в МГУ и в Московской горной академии, на базе шести факультетов которой позднее были созданы самостоятельные институты, в том числе Московский нефтяной институт (МНИ), который позже был получил имя ученого-геолога, академика И.М. Губкина.
В 1925 году Л.С. Лейбензон организовал первую в СССР нефтепромысловую лабораторию при Совете нефтяной промышленности. Плеяда учеников Л.С. Лейбензона создали и возглавили в разные годы кафедры нефтяного института: И.А. Чарный, возглавил в 1943г. кафедру теоретической механикой и гидравлики, затем создал в 1946г., кафедру общей и подземной гидравлики, впоследствии переименованную в кафедру нефтегазовой и подземной гидромеханики, которая сейчас является выпускающей и готовит теоретиков-вычислителей в области разработки и математического моделироавания. Именная стипендия, вручаемая каждый год студентам этой кафедры, носит имя И.А. Чарного. Именно И.А. Чарному принадлежит идея создания специального учебника по подземной гидромеханике, который до сих пор является теоретической базой научных разработок в области нефтегазового дела. Другой ученик Л.С. Лейбензона, также выпускник мехмата МГУ им. М.Л. Ломоносова В.Н. Щелкачев возглавил кафедру теоретической механики и до конца жизни проработал в нефтяном университете в качестве профессора.
Трудно переоценить влияние на развитие нефтегазовой теории в современном ее представлении основателя кафедры динамики (с 1951) и волновой динамики (1954), затем объединённых в кафедру газовой и волновой динамики, одного из создателей Института механики МГУ (1959) Х.А. Рахматуллина. Теория взаимопроникающих континуумов, позднее теоретически развитая его учеником Р.Н. Нигматуллиным, акад. РАН, в настоящее время возглавляющиv нашу кафедру является базовой платформой для описания течения многофазных многокомпонентных жидкостей в пористых средах. Более 50 учеников кафедр гидромеханики и газовой и волновой динамики стали преподавателями и научными сотрудниками РГУ нефти и газа и составили «боевой» костяк коллективов, создающих новые технологии разработки месторождений, которые не теряют связи с альма-матер.
На нашей кафедре читаются спецкурсы «Основы подземной гидромеханики» и «Прикладные задачи подземной гидромеханики», опирающиеся на работы классиков И.А. Чарного, В.Н. Щелкачева, Х.А. Рахматуллина, Р.Н. Нигматулина и ученых, работающих на нашей кафедре: Н.Н. Смирнова, А.В. Звягина, Киселева А.Б. и др.
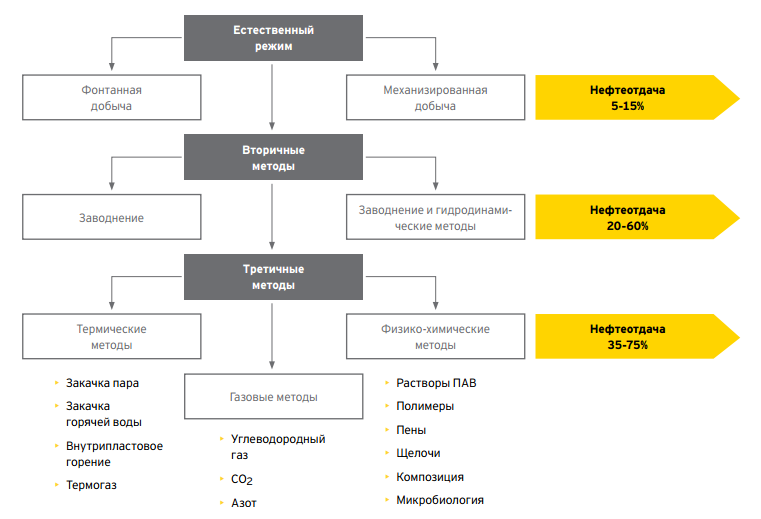
Каждое месторождение проходит несколько этапов жизни: разведка, создание проекта разработки, бурение, добыча на естественном режиме, использование методов повышения нефтеотдачи (Рис.3). На каждом этапе математическое моделирование является инструментом «изучения», «улучшения» и прогнозирования. Важным является получение аналитических и приближенных решений, требующих достаточно высокой математической культуры. Построение прогнозных решений, описывающих комплексно свойства конкретного месторождения требует решений системы дифференциальных уравнений нескольких подвижных фаз, реагирующих между собой и с пористой матрицей. Смачиваемость, капиллярные эффекты в совокупности с массовыми и поверхностными силами определяются способность различных фаз и компонент смеси двигаться по сети пористых каналов. Использование химических-активных флюидов, реагирующих с со скелетом пористой матрицы, требует современного подхода, основанного на рассмотрении структуры капиллярной системы, учета распределения пор по размерам и возможности его трансформации по мере протекания реакций взаимодействия.
В настоящее время помимо разработки традиционных месторождений нефти и газа, находящихся в поздней стадии разработки и уже значительно обводненных (метод вытеснения водой является наиболее простым и популярных методом повышения нефтеотдачи) актуальным является переход к новым, наукоемким методам воздействия на пласты. Чтобы найти новые технологические схемы, обосновать возможность их применения и эффективность нужно уметь строить адекватные математические модели и решать их численно, создавая собственные программные коды.
Перед нефтегазовой наукой стоит целый спектр нерешенных проблем по созданию моделей, сочетающих комплексно все свойства пластовых флюидов, закачиваемых активных жидкостей, трансформацию структуры пористой среды. Использование новейших полимерных субстанций, поверхностно-активных веществ, кислотных и взрывчатых составов- все еще требует глубокого изучения.
Отдельный блок задач касается разработки так называемых нетрадиционных месторождений: сланцевых пластов, керогеносодержащих коллекторов, газогидратных залежей. Эти темы рассматриваются как приоритетные направления развития нефтегазового инжиниринга и предлагаются студентам в качестве направлений научных исследований и выполнения выпускных дипломных работ.

Публикации:
- Кравченко М.Н., Ивлев М.И., Пантелей К.Д. Математическое моделирование сорбционных процессов с учетом трансформации пористой матрицы // Учен. зап. Казан. ун-та. Сер. Физ.-матем. науки. – 2021. – Т. 163, кн. 2. – С. 128–142.DOI
- Kravchenko M.N., Ivlev M. I., Dieva N.N. Hydrodynamic approach to the processing of core sample tests considering microstructural changes.// Journal of Physics: Conference Series, 2057 (2021). 012109 IOP Publishing.7 PP DOI
- Кравченко М.Н., Чидякина О.О. Гидродинамические аспекты поиска подходов к разработке газогидратных месторождений. Упругость и неупругость. Материалы Международного научного симпозиума по проблемам механики деформируемых тел, посвященного 110-летию со дня рождения А. А. Ильюшина (Москва, 20–21 января 2021 года) / Под ред. проф. Г. Л. Бровко, проф. Д. В. Георгиевского, проф. И. Н. Молодцова. — М.: Изд-во Моск. ун-та, 2021. — 552 с. С.491-498
- Kravchenko M.N., Dieva N.N., Fatykhov G.A. Hydrodynamic Analysis of Pyrolytic Studies for the Kerogen-Containing Rocks of Romashkinskoye Field. // Processes in GeoMedia 2021. Volume III. pp 273-284. DOI
- Аминев Д. А., Кравченко М. Н., Бадертдинова Е. Р. Определение фильтрационно-емкостных свойств нефтематеринских отложений методом численного решения обратных задач. Новые вызовы фундаментальной и прикладной геологии нефти и газа — XXI век: Материалы Всерос. науч. конф. с участием иностранных ученых, посв. 150-летию акад. АН СССР И. М. Губкина и 110-летию акад. АН СССР и РАН А. А. Трофимука / Ин-т нефтегаз. геологии и геофизики им. А. А. Трофимука СО РАН; Новосиб. гос. ун-т. Новосибирск : ИПЦ НГУ, 2021. — С 189-191.
- Кравченко М.Н., Диева Н.Н. Гидродинамический анализ эффективности циклического термогазохимического воздействия на месторождениях с генерационным потенциалом. Международная конференция «Математические идеи П. Л. Чебышёва и их приложения к современным проблемам естествознания», приуроченная к 200-летию со дня рождения великого русского математика, академика П. Л. Чебышёва : Материалы конференции. / (Обнинск, 14–18 мая; Сургут, 23–29 мая 2021 г.): Материалы конференции. Под ред. акад. В.Б. Бетелина. — Калуга: Калужский печатный двор, 2021. — 397 с. С 152-153.
- Aminev D.A., Kravchenko M.N. Determining reservoir parameters with nonisothermal real gas flow. //IOP Conference Series: Materials Science and Engineering. V 1201, 1, 2021. DOI
- Кравченко М.Н., Диева Н.Н., Разбегина Е.Г., Малова А.Д.. Моделирование фильтрационных процессов в нефтяном пласте с учетом экзотермической реакции разложения закачиваемого активного состава. Материалы всероссийской конференция молодых ученых-механиков (YSM-2021). Сочи, «Буревестник» МГУ, 3-12 сентября 2021 г. Сочи, «Буревестник» МГУ, 3-12 сентября 2021 г.
- Кравченко М.Н. Гидро-перколяционный подход к моделированию процессов адсорбции в пористых средах. Конференции «Ломоносовские чтения-2021». Секция «Механика».
- Кравченко М.Н., Бадертдинова Е.Р, Аминев Д.А. Учет нелинейных свойств пластового флюида при моделировании нестационарных фильтрационных процессов. 75 лет кафедре нефтегазовой и подземной гидромеханики: Сборник научных трудов. - М.: Издательский центр РГУ нефти и газа (НИУ) имени И.М.Губкина, 2021, 233 с. С 135-142.
МОДЕЛИРОВАНИЕ ГИДРОРАЗРЫВА ПЛАСТА
проф., д.ф.-м.н. Н.Н. Смирнов, проф., д.ф.-м.н. А.В. Звягин, доцент, к.ф.-м.н. А.А. Шамина, инженер Д.А. Пестов
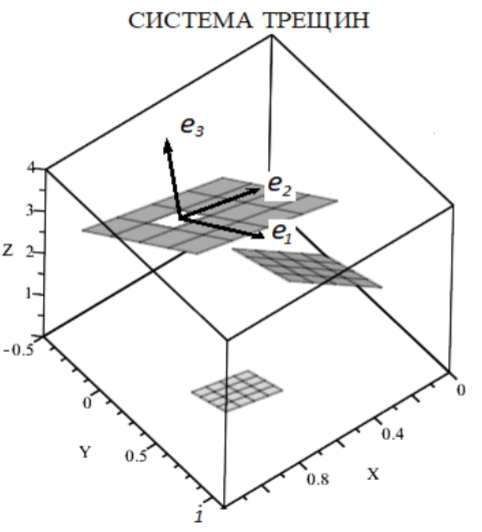
на граничные элементы.
Гидроразрыв пласта – один из основных способов увеличения добычи нефти и газа на месторождениях. Для его проведения сквозь специальные отверстия в скважине в окружающую породу под большим давлением подаётся жидкость, которая разрывает породу, образуя трещину. Затем вместе с жидкостью вводят проппант – набор мелких твёрдых крупинок (раньше для этих целей, например, использовали песок) которые остаются в трещине после того как жидкость гидроразрыва откачают и не дают трещине закрыться. Подобная трещина является областью повышенной проницаемости, что создаёт путь, по которому в скважину потом легко сможет поступать нефть, которую начнут выдавливать из пласта, подавая воду через другие скважины. Моделрование процесса гидроразрыва является сложной задачей, требующей совместного решения задач из различных областей: динамики многофазной вязкой жидкости в канале с подвижными стенками, механики упругости и разрушения, а также теории фильтрации.
Трёхмерное моделирование трещины гидроразрыва позволяет рассматривать рост трещины и его взаимодействие с произвольно ориентированными дефектами среды, не прибегая к упрощениям, неизбежно снижающим точность модели. Разработанный сотрудниками кафедры под руководством профессора, д.ф.-м.н. Звягина А.В. граничноэлементный метод решения задачи взаимодействия трещины гидроразрыва с природными разломами [3] позволяет понизить вычислительную размерность задачи, за счет того, что на элементы разбивается не среда, а только поверхность трещин (Рис.1). Это возможно благодаря использованию полученных аналитических решений уравнений теории упругости.
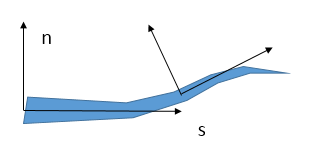
и соответствующие системы координат.
Под влиянием неоднородностей среды часто возникает ситуация, когда трещина не продолжает расти в своей плоскости, а поворачивает, что существенно влияет на её итоговое расположение и параметры. Построенная модель роста неплоской трещины гидроразрыва позволяет учитывать отклонение трещины от изначальной плоскости (Рис 2). Этот эффект может быть важен при оценке взаимодействия трещины гидроразрыва с естественными разломами. При приближении к естественному разлому или другой трещине, трещина гидроразрыва может заметно отклоняется от предыдущего направления, что в некоторых ситуациях предотвращает подобное пересечение, а в некоторых ускоряет его [1].
Важными задачами для моделирования гидроразрыва являются также определение начальных условий для роста трещины [4,5], поскольку при начало раскрытия трещины является сингулярной точкой для данной задачи, а также определение влияния неоднородных механических свойств среды на рост трещины [2].
Публикации:
- Взаимодействие статической трещины гидроразрыва, находящейся под постоянным давлением жидкости, с природным разломом / А. В. Акулич, А. В. Звягин, Д. А. Пестов и др. // Математическое моделирование. — 2018. — Т. 30, № 7. — С. 79–92.
- Моделирование течения жидкости в трещине гидроразрыва неоднородно трещиностойкого пласта в плоско-трехмерной постановке / А. Б. Киселев, Л. Кайжуй, Н. Н. Смирнов, Д. А. Пестов // Известия Российской академии наук. Механика жидкости и газа. — 2021. — № 2. — С. 15–28. DOI
- Численный метод разрывных смещений в пространственных задачах механики трещин / А. В. Звягин, А. А. Лужин, Д. И. Панфилов, А. А. Шамина // Известия Российской академии наук. Механика твердого тела. — 2021. — № 1. — С. 148–162. DOI
- Li K. R., Smirnov N. N., Qi C. Z., Kiselev A. B. An approximate analytical solution for hydraulic fracture opening under non-uniform internal pressure // Materials Physics and Mechanics. 44 (2020) 288-305. DOI
- 5. Li K. R., Smirnov N. N., Qi C. Z., Kiselev A. B., Pestov D. A. The numerical asymptotic solution to initial condition problem of pre-existing plane-strain hydraulic fracture with fluid lag // Engineering Fracture Mechanics. 2020: 107296. DOI