Течения жидкостей со сложной pеологией
к.ф.-м.н. О.А. Логвинов, асп. Л.А. Паремкая
Общие законы сохранения механики сплошных сред справедливы для произвольного континуума и потому образуют, вообще говоря, незамкнутую систему уравнений. Для замыкания системы законов сохранения необходимо конкретизировать среду – записать определяющие её соотношения, называемые для жидкостей уравнениями состояния. Задачей определения подобных (реологических) соотношений для реальных жидкостей и газов занимается дисциплина на стыке физики, химии и механики, называемая реологией.
В отличие от законов сохранения механики сплошных сред, которые просто постулируются, получить реологические соотношения возможно только на основе экспериментальных данных, статистической физики или химического анализа вещества. Как правило, подобные соотношения представляют собой алгебраические или дифференциальные связи между внутренними напряжениями и кинематическими переменными (в конечном счёте, полем скорости, возможно, зависящем и от времени). Существуют уравнения состояния и другого вида – термодинамические и энергетические.
Простейшей реологической моделью, подходящей для многих жидкостей и газов (вода, воздух, нефть, глицерин), является модель ньютоновской жидкости. Нагляднее всего представлять реологические модели при помощи так называемой кривой течения – графика зависимости между напряжением и скоростью сдвига (деформации) в одномерном случае. Для ньютоновской (линейно вязкой) жидкости кривая течения представляет собой прямую в плоскости скорость сдвига-напряжение (Рис. 1а), тангенс угла наклона которой равен (постоянной) динамической вязкости.
Поведение реальных жидкостей часто не соответствует идеализированной линейной кривой течения. Неньютоновскими жидкостями называют среды с нелинейными кривыми течения, в том числе зависящими и от времени. Подобное определение является чересчур общим и нуждается в дальнейших уточнениях. Принципиально неньютоновские жидкости можно разбить на три большие группы:
- жидкости, для которых скорость сдвига в данной точке представляется некоторой функцией только напряжения сдвига в той же точке.
- жидкости, для которых связь между напряжением и скоростью сдвига зависит также и от времени действия напряжения или от предыстории деформирования.
- вязкоупругие жидкости, обладающие свойствами как твёрдого тела, так и жидкости, и частично проявляющие упругое восстановление формы после снятия напряжений.
Вязкие неньютоновские жидкости, характеристики которых не зависят от времени (первая группа), делятся, в свою очередь, на три подгруппы: бингамовские, псевдопластические и дилатантные жидкости.
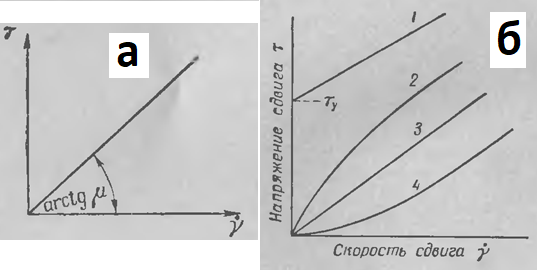
(а) линейная кривая для ньютоновской жидкости.
(б) различные нелинейные кривые для неньютоновских
жидкостей.
Кривая течения для бингамовской жидкости представлена на Рис. 1б под номером (1). В отличие от ньютоновского случая, жидкость Бингама обладает пределом текучести, превышение которого приводит к возникновению вязкого течения. При меньших напряжениях возможно только движение жидкости как абсолютно твёрдого тела, то есть скорости деформаций равны нулю.
Примеры бингамовских жидкостей: шлам, буровой раствор, масляная краска, зубная паста.
Кривая течения для псевдопластических жидкостей такова, что отношение напряжения сдвига к скорости сдвига (кажущаяся вязкость) уменьшается с ростом скорости сдвига (Рис. 1б, кривая 2).
Примеры псевдопластических жидкостей: суспензии с асимметричными частицами, высокополимерные растворы (например, производные целлюлозы), некоторые нефти.
Кривая течения для дилатантных жидкостей такова, что кажущаяся вязкость увеличивается с ростом скорости сдвига (Рис. 1б, кривая 4).
Примеры дилатантных жидкостей: суспензии с большим содержанием твердой фазы, крахмальные клейстеры, мокрый песок.
Кажущаяся вязкость может определяться не только скоростью сдвига, но и его продолжительностью (вторая группа неньютоновских жидкостей). В этом случае жидкости делятся на два класса – тиксотропные и реопектические – в зависимости от того, убывают или возрастают со временем напряжения сдвига при постоянной деформации.
При деформировании тиксотропного материала из состояния покоя с постоянной скоростью сдвига его структура постепенно разрушается, а кажущаяся вязкость убывает со временем. Тиксотропия является обратимым процессом и после исчезновения возмущений жидкости её структура постепенно восстанавливается. Тиксотропия, в основном, напоминает псевдопластичность, когда временем, необходимым для связывания частиц, нельзя пренебрегать.
Реопектические материалы встречаются реже: им свойственно постепенное структурообразование при сдвиге, хотя обычно сдвиг способствует разрушению структуры. В результате кажущаяся вязкость реопектических материалов возрастает со временем. Однако, несомненно, существует критическая величина сдвига, после превышения которой происходит разрушение структуры. Реопектические жидкости, в общем, сходны с дилатантными.
Вязкоупругой называется жидкость, проявляющая как упругое восстановление формы, так и вязкую текучесть (третья группа неньютоновских жидкостей). В самом простом случае вязкая составляющая характеризуется законом Ньютона, а упругая – законом Гука.
Примеры вязкоупругих жидкостей: смолы, бентонитовые глины.
На практике, реальные жидкости часто демонстрируют сложное реологическое поведение, при котором одновременно сочетаются различные неньютоновские свойства. Жидкости гидроразрыва (пропанты), например, практически всегда являются нелинейно-вязкими, обладают пределом текучести и проявляют, помимо прочего, упругие свойства. Особенно важным является учёт неньютоновских свойств жидкостей в биомеханике и медицине. Рассмотрение реологии крови – важный раздел гемодинамики, изучающей движение крови по сердечно-сосудистой системе. Таким образом, применение простейшей ньютоновской реологической модели оказывается недостаточным для моделирования многих реальных течений.
Литература:
- Уилкинсон У. Л. Неньютоновские Жидкости. 1964. М.: Мир.
- Астарита Дж., Марруччи Дж. Основы Гидромеханики Неньютоновских Жидкостей. 1978. М.: Мир.