проф., д.ф.-м.н. А.В. Звягин, доцент, к.ф.-м.н. А.А. Лужин, доцент, к.ф.-м.н. А.А. Шамина, к.ф.-м.н. Д.И. Панфилов

Одной из важнейших характеристик любого материала является его прочность. Но сразу же возникает множество вопросов. Что нужно понимать под словом «прочность»? Какой критерий прочности применять? Ответы, в свою очередь, существенно зависят от технологии изготовления детали конструкции, условий её эксплуатации, степени агрессивности внешней среды и т.д. и т.п. Также довольно сильно на характеристики различных инженерных материалов и горных пород влияют дефекты, неизменно присутствующие в структуре исследуемых сред, а также появляющиеся при различных действиях с исследуемыми объектами. Наличие микродефектов приводит к необходимости пересмотра и доработки критериев прочности и разрушения твердого деформируемого тела. Разделом механики, занимающейся этими вопросами, является линейная механика разрушения или «механика трещин». Базовыми объектами изучения линейной механики разрушения являются поры, трещины, границы кристаллов и т.д. Термин «трещина» подразумевает моделирующий её разрыв поля перемещений на отрезке линии (в плоской задаче) или на некоторой части поверхности (в пространственной задаче). Рассмотрение прочности в рамках теории упругости обусловлено инженерными требованиями недопустимости развитых областей пластического течения. Не случайно в курсах «сопротивление материалов» в качестве силовых критериев прочности часто используются пределы упругости. Однако, набор задач, в которых найдено аналитическое решение, чрезвычайно мал и включает в себя лишь задачи с малым количеством трещин либо задачи с периодической системой трещин. Сведение задачи к периодической структуре обусловлено не только возможностью получения точного решения, но и особенностями эволюции разрушения. Показано, что возникновение одной трещины приводит к формированию периодической структуры вторичных трещин. Одновременно с этим для приложений важно учитывать специфику задач механики разрушения и иметь возможность точно смоделировать поведение среды в малой окрестности границ трещин. Все это ведет к жестким требованиям, налагаемым на точность численных решений подобных задач. В связи с этим можно выделить активно развиваемые сотрудниками кафедры бессеточные методы граничных элементов, при работе которых на элементы разбивается не вся область, а лишь ее граница.

Задачи механики разрушения имеют специфику. В них, важнейшими характеристиками решения, подлежащими определению, являются коэффициенты интенсивности напряжений, которые характеризуют особенности поведения напряжений в окрестности границ трещины. Для приложений важно уметь отвечать на вопрос: будет ли разрушаться материал при наличии в нем трещины или системы трещин при заданных нагрузках. И одним из критериев роста трещины является силовой критерий Ирвина. Он заключается в сравнении коэффициентов интенсивности напряжений для трещины, получающихся при данной нагрузке, и критических коэффициентов интенсивности напряжений конкретного материала. Точное определение этих коэффициентов является наиболее сложной проблемой при численной реализации решения задачи разрушения.

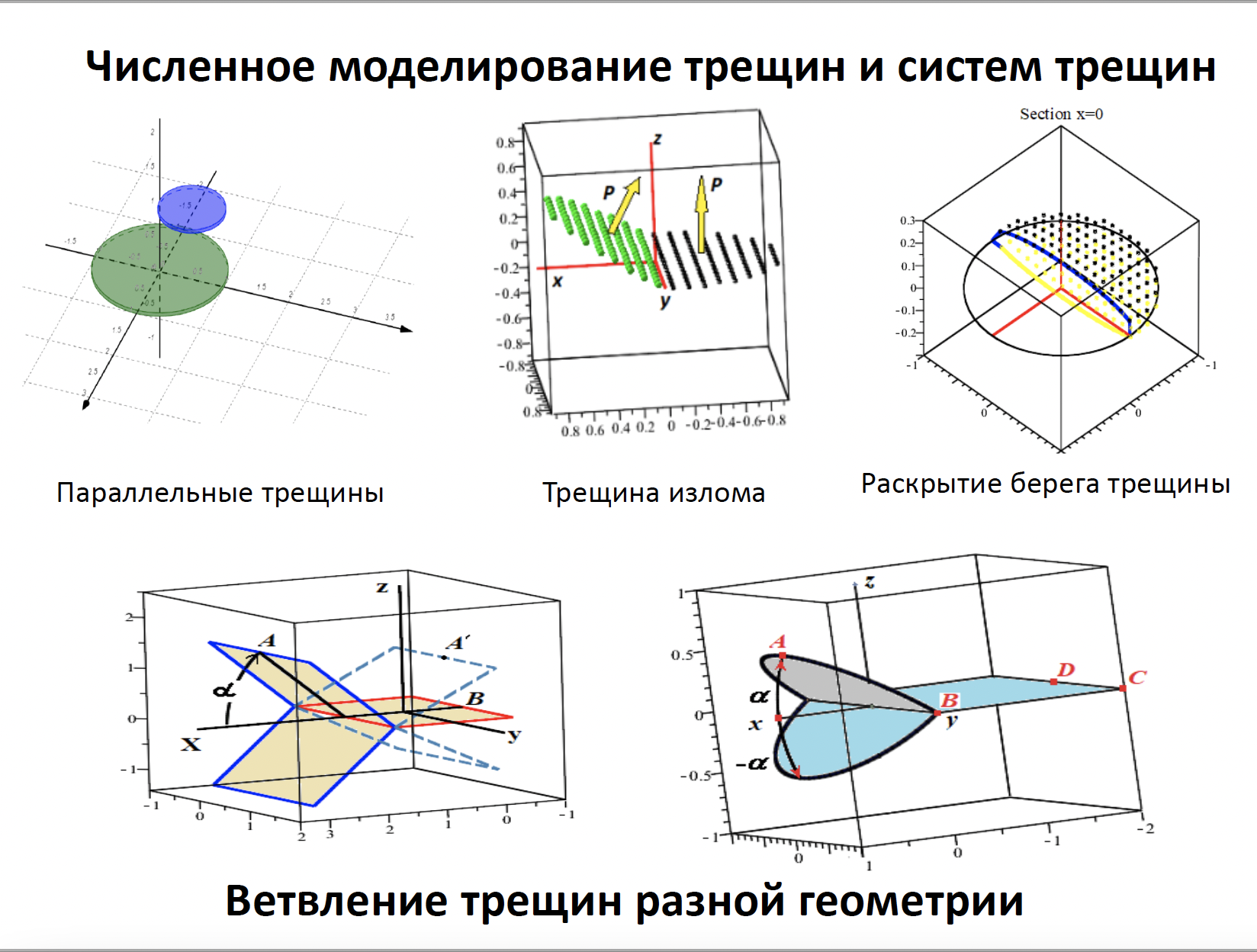
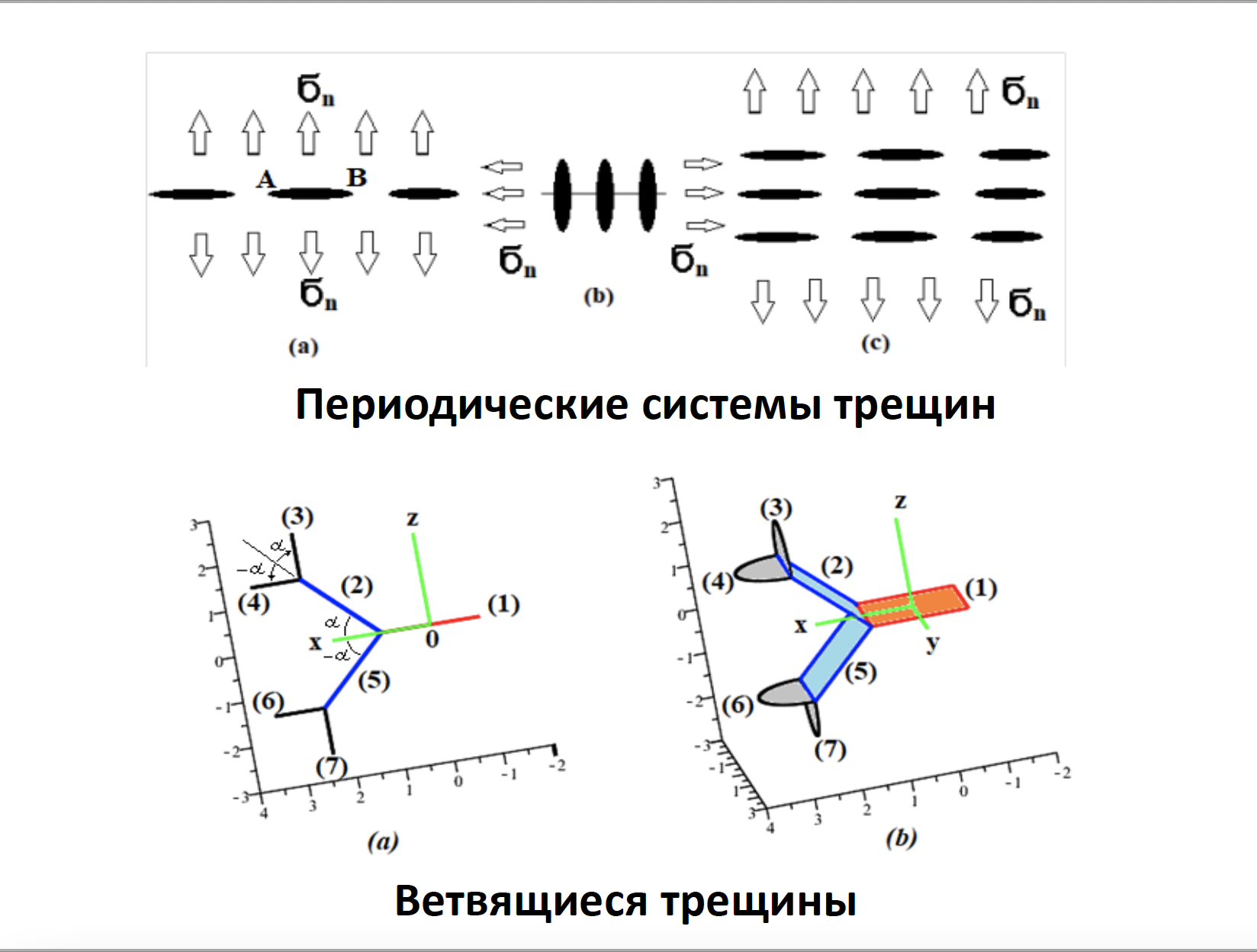
Разработанные сотрудниками кафедры алгоритмы численного решения задач механики трещин были использованы при решении прикладных плоских и пространственных задач механики трещин. Предложенные методы моделирования сред, ослабленных вообще говоря произвольно ориентированной системой трещин, позволяют рассматривать сложные конфигурации больших систем трещин и находить коэффициенты интенсивности напряжений с высокой точностью. А подход, позволяющий, учитывая периодичность рассматриваемой структуры, свести проблему к решению задачи для ограниченного числа трещин, предоставляет возможность анализировать напряженно-деформируемое состояние сред с бесконечным числом трещин.

Публикации:

1. Zvyagin A.V., Luzhin A.A., Panfilov D.I., Shamina A.A. Numerical Method of Discontinuous Displacements in Spatial Problems of Fracture Mechanics //J. Mechanics of Solids. Allerton Press Inc. (United States). V. 56, 2021. P. 119-130 DOI
2. Zvyagin A.V., Luzhin A.A., Smirnov N.N., Shamina A.A., Shamin A.Y. Stress intensity factors for branching cracks in space structures //J. Acta Astronautica, Pergamon Press Ltd. (United Kingdom), V. 180, p. 66-72 DOI
3. Shamina A.A., Zvyagin A.V., Smirnov N.N., Luzhin A.A., Panfilov D.I., Udalov A.S. Computational modeling of cracks different forms in three-dimensional space //Acta Astronautica. Pergamon Press Ltd. (United Kingdom). 2021 DOI
4. Zvyagin A.V., Udalov A.S. A Displacement Discontinuity Method of High-Order Accuracy in Fracture Mechanics // Moscow University Mechanics Bulletin, Allerton Press Inc. (United States), 2020, V. 75, № 6, p. 153-159 DOI
5. Shamina A.A., Zvyaguin A.V., Akulich A.V., Tyurenkova V.V., Smirnov N.N. The study of the strength of structures weakened by a system of cracks // Acta Astronautica, Pergamon Press Ltd. (United Kingdom), 2020. V. 176, p. 620-627 DOI
6. Zvyagin A.V., Panfilov D.I., Shamina A.A. The Mutual Influence of Disk-Shaped Cracks in Three-Dimensional Elastic Space // Moscow University Mechanics Bulletin, Allerton Press Inc. (United States), 2019. V. 74, № 4, p. 89-96 DOI
7. Zvyagin A. V., Udalov A. S., Shamina A. A. Boundary element method for investigating large systems of cracks using the williams asymptotic series // Acta Astronautica, Pergamon Press Ltd. (United Kingdom), 2022, V. 194, p. 480-487 DOI